This builds on my post about estimating pi, to examine a method for calculating pi that was used by Archimedes around 250BC. Despite doing maths most days, I’ve never tried this before – it was great fun!
In calculating pi, firstly I will look at strategy, and then details/process which require sound understanding of GCSE trigonometry, with points of interest for AS and A level students.
The method identifies upper and lower bounds, between which pi must lie. The premise is that the circumference of a circle must lie between the perimeter of two regular hexagons, one drawn inside the circle (inscribed), the other drawn outside the circle (circumscribed).

You should pause to confirm this is true.
Let the circle have radius r , diameter 2r .
The inscribed hexagon comprises 6 equilateral triangles, each with side length r . The perimeter of the inscribed hexagon is then 6r.
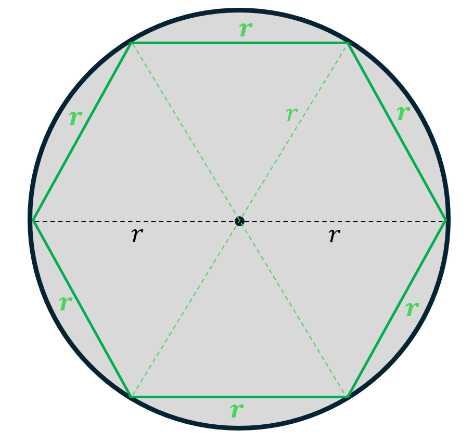
This green perimeter is smaller than the circumference of the circle, so we know 6r < C. Since pi is the ratio of circumference to diameter of a circle C/D,

To obtain the perimeter of the circumscribed circle, I used right-angled triangle trigonometry:
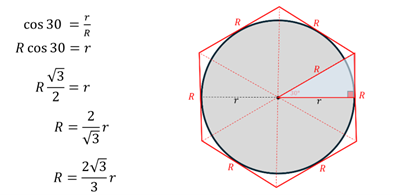
This gives perimeter of the hexagon as
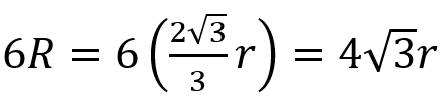
The circumference of the circle is smaller than this red perimeter, so we know that C is less than this. Since pi is the ratio of circumference to diameter of a circle C/D,

So, we have our first interval for pi:

SOHCAHTOA is from GCSE maths and knowing the exact value of cos 30 is on some GCSE specs for non-calculator papers. Rationalising surds is an AS level maths skill.
To obtain a smaller range for pi, Archimedes then doubled the number of sides from 6 to 12, then 24, 48 etc. If you’re working at a high level in GCSE and/or you’re an aspiring A level maths student, you could try to recreate the same logic to obtain new bounds. There are many ways to do this, but I switched to using the cosine rule to find the new contributions to the perimeter of the smaller & larger 12-sided polygons. At some point you’ll need cos 15 which you can of course get from your calculator, but if you’re in the second year of A level maths you could obtain this by applying the compound angle formula for cos (A-B) with cos (45-30) using exact values for trig ratios of 45 & 30.
I will post my own workings later this week, but with 12 sides to four decimal places you get a much smaller interval for pi (3.141592.. ). You’re aiming for:
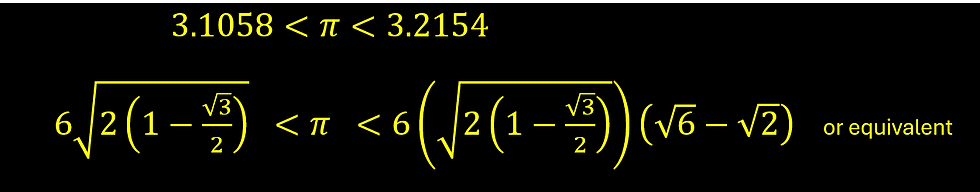
To keep exact surds, you’ll need AS level skills from the start of Year 12. And I’m thinking you could write an algorithm to generate increasingly accurate bounds? I challenge you to have a go, whether you’re a student/teacher, or just have an interest in solving maths puzzles. Good luck!!

Kommentarer